🧬 nonlinear-causal 
nonlinear-causal is a Python module for nonlinear causal inference, including hypothesis testing and confidence interval for causal effect, built on top of instrument variables and Two-Stage least squares (2SLS).
GitHub repo: https://github.com/nl-causal/nonlinear-causal
Paper: PMLR@CLeaR2024
Documentation: https://nonlinear-causal.readthedocs.io
Models
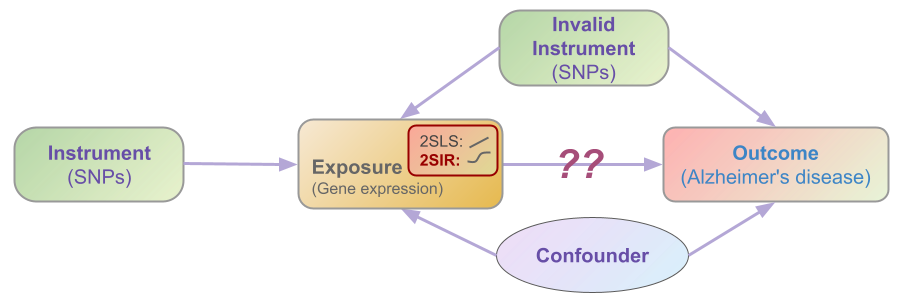
nonlinear-causal considers two instrument variable causal models:
Illustrated by the above image example, let’s denote \(\mathbf{z}\) as the valid/invalid instrument variables (such as SNPs), \(x\) as the exposure (such as gene expression), and \(y\) as the outcome (such as AD).
Two-Stage least squares (2SLS)
where \((w,\varepsilon)\) are the error terms independent of the instruments \(\mathbf{z}\), however, \(w\) and \(\varepsilon\) may be correlated due to underlying confounders, and \(\beta\in\mathbb{R}\), \(\mathbf{\alpha}\in\mathbb{R}^p\), \(\mathbf{\theta}\in\mathbb{R}^p\) are unknown parameters.
Two-Stage Sliced Inverse Regression (2SIR)
where \((w,\varepsilon)\) are the error terms independent of the instruments \(\mathbf{z}\), however, \(w\) and \(\varepsilon\) may be correlated due to underlying confounders, and \(\beta\in\mathbb{R}\), \(\mathbf{\alpha}\in\mathbb{R}^p\), \(\mathbf{\theta}\in\mathbb{R}^p\) are unknown parameters.
Remarks
2SLS / 2SIR. \(\mathbf{\alpha} \neq \mathbf{0}\) indicates the violation of the second and/or third IV assumptions. The models may not be identifiable with the presence of invalid IVs. In the literature, additional structural constraints are imposed to avoid this issue, such as \(\|\mathbf{\alpha}\|_0 < p/2\).
2SIR. \(\beta\) and \(\phi\) are identifiable by fixing \(\|\mathbf{\theta}\|_2 = 1\) and \(\beta \geq 0\).
Strengths of 2SIR
Model assumptions of 2SIR are weaker than the classical 2SLS: the model admits an arbitrary nonlinear transformation \(\phi(\cdot)\) across \(\mathbf{z}\), \(x\) and \(y\), relaxing the linearity assumption in the standard TWAS/2SLS.
2SIR includes 2SLS and Yeo-Johnson power transformation 2SLS (PT-2SLS) as special cases. It is worth mentioning that the proposed method remains competitive against 2SLS/PT-2SLS even if the linear assumption holds.
The implicit linear structure in both 2SLS and 2SIR allows the use of GWAS summary data of our method, in contrast to requiring individual-level data by the other (non-linear) models.
What We Can Do:
2SLS
Estimate \(\beta\): marginal causal effect from \(X \to Y\)
Hypothesis testing (HT) and confidence interval (CI) for marginal causal effect \(\beta\).
2SIR
Estimate \(\beta\): marginal causal effect from \(X \to Y\)
Hypothesis testing (HT) and confidence interval (CI) for marginal causal effect \(\beta\).
Estimate nonlinear causal link \(\phi(\cdot)\).
For implementation usage of nonlinear_causal, kindly refer to the provided examples and notebooks.
Installation
# Install the latest version `nonlinear-causal` in Github:
pip install git+https://github.com/nl-causal/nonlinear-causal
# or Install `nonlinear-causal` lib from `pypi`
pip install nonlinear-causal
Examples and notebooks
Simulation Performance
We examine four cases: (i) \(\beta = 0\), (ii) \(\beta = .05\), (iii) \(\beta = .10\), (iv) \(\beta = .15\). Note that case (i) is for Type I error analysis, while \(\beta > 0\) in (ii) - (iv), suggests power analysis.
Six transformations are considered: (1) linear: \(\phi(x) = x\); (2) logarithm: \(\phi(x) = \log(x)\); (3) cube root: \(\phi(x) = x^{1/3}\); (4) inverse: \(\phi(x) = 1/x\); (5) piecewise linear: \(\phi(x) = xI(x\leq 0) + 0.5 x I(x > 0)\); (6) quadratic: \(\phi(x) = x^2\).
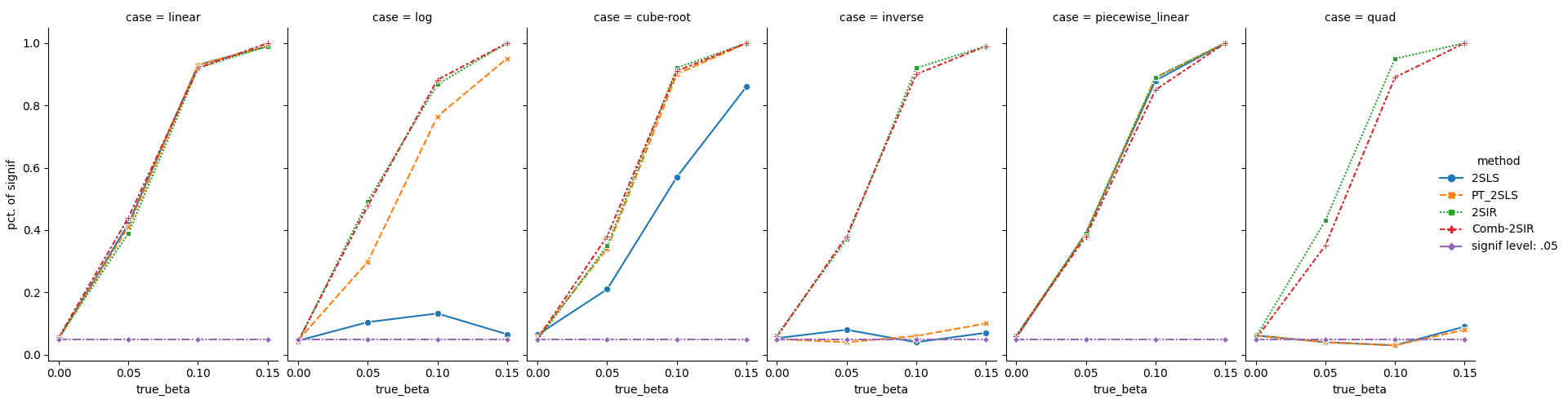
For more information, please check our paper (Section 3) or the Jupyer Notebook for the simulation examples.
Reference
If you use this code please star 🌟 the repository and cite the following paper:
Dai, B., Li, C., Xue, H., Pan, W., & Shen, X. (2024). Inference of nonlinear causal effects with GWAS summary data. In Conference on Causal Learning and Reasoning. PMLR.
@inproceedings{dai2022inference,
title={Inference of nonlinear causal effects with GWAS summary data},
author={Dai, Ben and Li, Chunlin and Xue, Haoran and Pan, Wei and Shen, Xiaotong},
booktitle={Conference on Causal Learning and Reasoning},
pages={},
year={2024},
rganization={PMLR}
}